В МГТУ заработал новый четырёхкубитный российский квантовый процессор
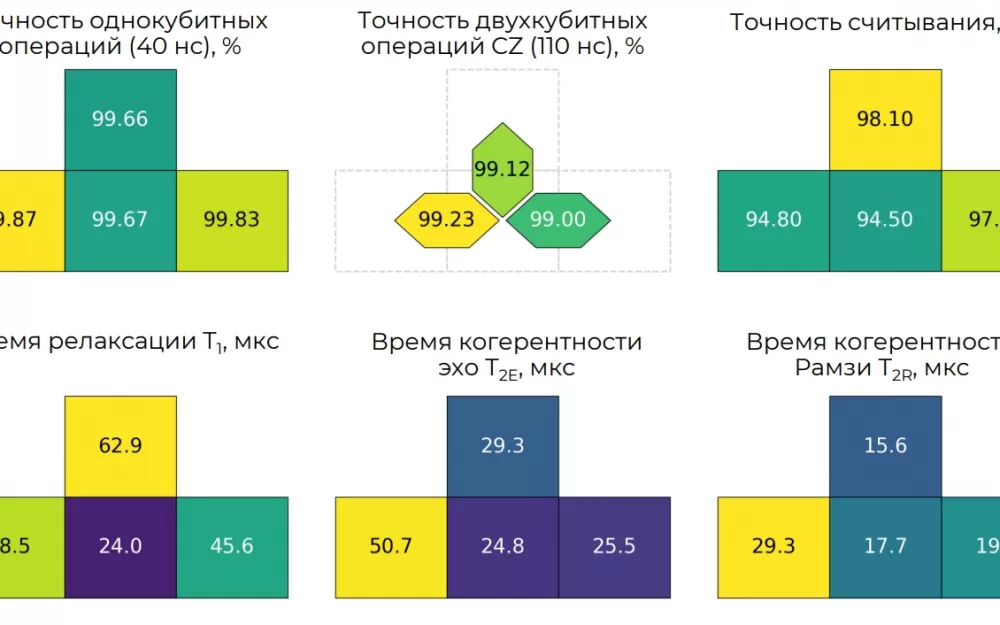
В совместном центре МГТУ им. Н.Э. Баумана и ФГУП «ВНИИА им. Н.Л. Духова» заработал первый российский высокоточный сверхпроводниковый квантовый процессор Snowdrop 4Q, рассказали в Научно‑образовательном центре «Функциональные Микро/Наносистемы» МГТУ им. Н.Э. Баумана . Средняя точность однокубитных операций процессора составила 99,76%, двухкубитных операций — 99,11%, точность считывания — 96,18%. Достигнутые параметры процессора позволили реализовать серию сложных алгоритмов. На квантовом сопроцессоре была смоделирована намагниченность цепочки спинов , решено уравнение теплопроводности и реализован алгоритм решения систем линейных уравнений, что прокладывает путь к дальнейшему практическому применению квантовых вычислителей.
По словам разработчиков, озвученные показатели стали рекордным для российских многокубитных систем при реализации ряда сложных квантовых алгоритмов. Архитектура процессора основана на перестраиваемых по частоте кубитах‑трансмонах с управляемой связью между кубитами. Чипы квантовой элементной компонентной базы изготовлены по серийной технологии НОЦ ФМН.
Для штатной работы процессора в составе суперкомпьютера идёт сложная процедура настройки и калибровки, занимающая длительное время и использующая алгоритмы машинного обучения для определения оптимальных параметров управляющих сигналов. На первом этапе команде необходимо охарактеризовать процессор (измерить параметры качества кубитов). Сначала работают с каждым кубитом индивидуально: приводят в возбуждённое состояние и «снимают мерки», включая время релаксации T1 (время, за которое кубит переходит из возбуждённого в основное состояние) и время когерентности T2 (время, в течение которого кубит сохраняет квантовую информацию). Время T2 включает два типа — это Рамзи (чувствительное ко всем видам шумов) и эхо (не чувствительное к низкочастотным шумам).
Далее следует итеративная и многоэтапная процедура калибровки однокубитных и двухкубитных квантовых логических операций – составляющих квантового алгоритма. При калибровке точности однокубитных операций сначала работают с каждым кубитом отдельно, приводя все соседние кубиты в состояние покоя. Но уже сразу после калибровки всех кубитов поодиночке оптимизируют точность однокубитных операций при одновременной работе соседних кубитов. Именно так – одновременно – кубиты должны работать в практически полезных алгоритмах, и именно эту точность необходимо учитывать при сравнении квантовых процессоров. На следующем этапе оперируют парами кубитов для калибровки двухкубитных операций. В ходе калибровки оценивается точность однокубитных и двухкубитных операций, а также точность считывания. Только проведя полную характеризацию системы можно сказать, насколько процессор готов к настоящей работе. На процессоре НОЦ ФМН среднее время релаксации кубитов (T1) составило 47,7 микросекунды, время когерентности (T2) – 32,5 микросекунды, при длительности однокубитных операций 40 наносекунд, двухкубитных операций (CZ) 110 наносекунд.
Над калибровкой и полной характеризацией квантовой системы специалисты НОЦ ФМН работали последние три месяца. Точности логических операций, которых достиг чип архитектуры Snowdrop 4Q с высококогерентными кубитами (Scientific Reports volume 14, 7326 (2024)), позволили провести целую серию экспериментов, каждый из которых в перспективе направлен на решение практических задач центра.
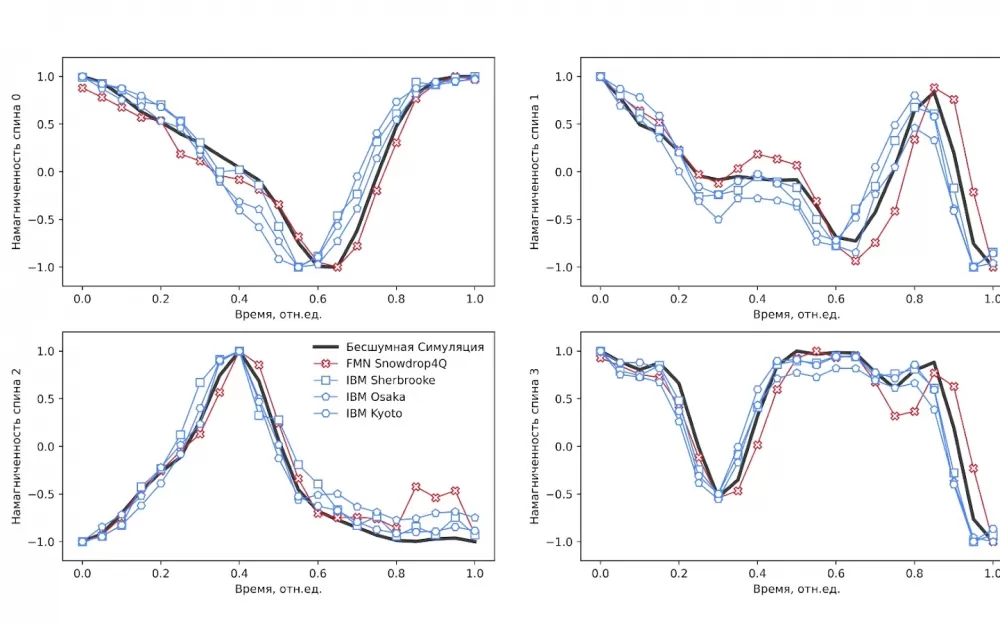
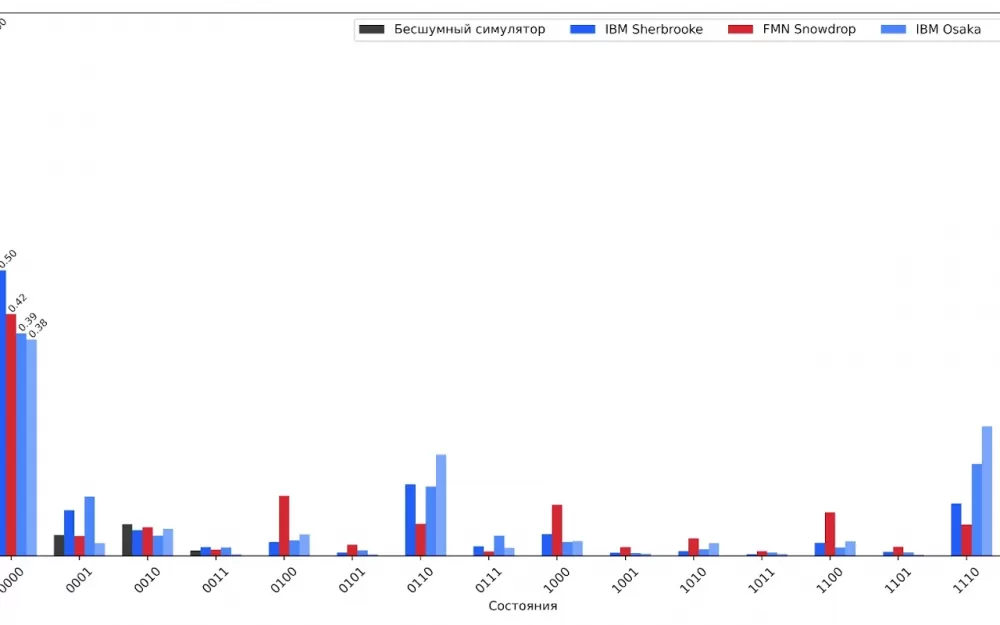
Команде алгоритмистов ФГУП «ВНИИА им. Н.Л. Духова» удалось провести на квантовом процессоре симуляцию динамики системы из четырёх спинов (модель Изинга в поперечном поле) для решения задач в области квантового магнетизма. В рамках эксперимента учёные опробовали собственный метод смягчения ошибок (error mitigation), основанный на нейросетевом обучении (Quantum Inf Process 21, 93 (2022). В качестве бенчмаркинга реализованные алгоритмы были опробованы на 127-кубитных процессорах IBM в облачном доступе. По итогам сравнения процессор Snowdrop 4Q показал сопоставимые по достоверности результаты алгоритмов (fidelity).
Помимо этого, на процессоре Snowdrop 4Q реализована оригинальная модификация сложного квантового алгоритма Харроу-Хассидима-Ллойда (HHL) из более 100 квантовых логических операций для численного решения системы линейных уравнений (Phys. Rev. A 107, 042408 (2023)). Этот алгоритм особенно требователен к точности операций и считывания квантовых процессоров.














Написать комментарий